Immersed body technique with applications
"We want to bring CFD to bear upon interdisciplinary problems in
engineering and science" - Neelesh Patankar
engineering and science" - Neelesh Patankar
Applications
(Click on images for specific projects)
Brief history of the field
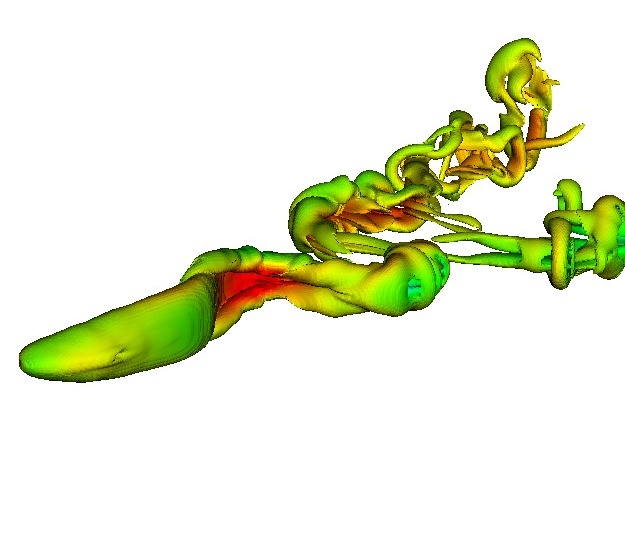
Fully resolved simulation techniques for immersed bodies in fluids are those in which fluid flow around each individual body is fully resolved without the use of approximate governing equations or models such as drag laws. The immersed objects can be rigid, elastic, or self-propelling bodies. After fluid flow simulation techniques matured, a substantial interest in fully resolved techniques for freely–moving rigid particle flows arose by the mid 1990s followed by a similar interest in freely–moving elastic and self–propelling bodies by the mid 2000s. Primary challenges were:
- Fluid equations had to be solved on a changing domain since the immersed bodies move.
- Coupling between the fluid and the immersed body should be fully resolved without using any modeling assumptions, such as drag laws.
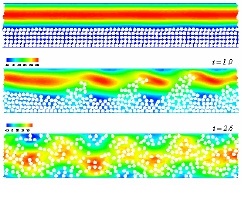
Early fully resolved techniques for rigid particulate flows had grids that moved with the bodies. However, this approach was computationally expensive, especially in three–dimensional problems. A fundamentally different paradigm, based on non–moving grids was developed for these problems, to which we have made crucial contributions.
Our contributions and innovations
I. Fully resolved constraint formulation for rigid & self–propelling bodies
Our method relies upon the idea of treating the entire domain as a fluid. The ‘fluid’ overlapping with the body domain is then constrained to move with specified deformation kinematics (e.g., for a rigid body the deformation kinematics would be zero). To do so, novel constraint–based governing equations were formulated. It was shown that the constraint gives rise to a Lagrange multiplier stress field. This stress field is as fundamental as the formulation of pressure due to the divergence–free constraint for an incompressible fluid. The governing equations can be easily implemented by immersed boundary–type techniques allowing application to arbitrary geometric configurations.
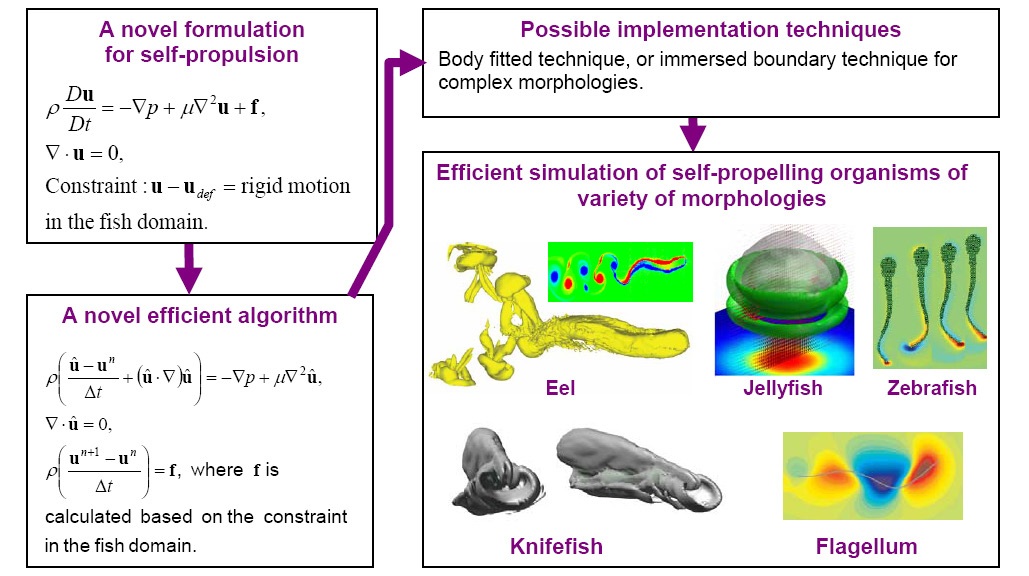
II. Fast projection algorithm for rigid & self–propelling bodies
This innovation pertains to a fast and efficient fractional time stepping algorithm to implement the governing equations of the new constraint–based formulation. This algorithm to impose the constraint in our problems is as fundamental as Chorin–type schemes for the incompressibility constraint (Chorin scheme was a major advance in the history computational fluid dynamics). Our approach is non-iterative and it reduces the computational cost by one-fourth compared to prior moving mesh techniques. Presently, this is the fastest rigid projection scheme for general unsteady fluid–particle problems.
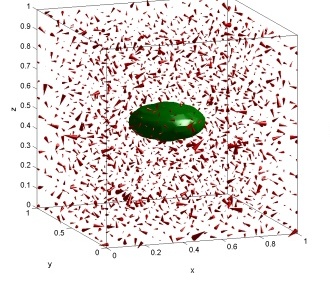
III. Novel approach for fully resolved simulations of Brownian systems
A novel approach to simulate Brownian motion at mesoscales was developed. In our approach thermal fluctuations are imposed in the fluid, unlike prior Brownian or Stokesian dynamics methods. This was the first Navier–Stokes equation–based approach of its kind. It has been fully validated for a variety of particle concentrations and shapes, for translational and rotational motions, etc.
Uniqueness, impact on the field, and outlook
We have developed a unified mathematical framework using a constraint–based paradigm for fully resolved simulation of a class of problems ranging from sub–micron scale Stokes flow to meter–scale turbulent flow conditions. The key strengths are computational efficiency and the ability to easily handle complex and deformable configurations. The computational framework is such that it is possible to introduce incremental modular changes to a fluid solver to make it capable of simulating rigid, elastic, or self-propelling bodies with or without thermal motion (i.e. Brownian motion). This class of techniques will be reviewed by us in an upcoming Annual Review of Fluid Mechanics article.
Our technique for rigid bodies is one of the basic fully resolved approaches that is applicable to a wide variety of problems including industrial processes such as fluidized beds, sediment transport in oil recovery as well as in geomorphic processes, colloidal systems, intra–cellular Brownian systems such as motor proteins, protein–protein binding kinetics, computational drug discovery, and even geophysical simulations of volcanic systems. The latest work on self–propelling organisms is emerging as one of the leading techniques of the type and the only one that has been tested against live swimming data. Its impact pertains to applications in interdisciplinary areas such as designing novel biomimetic underwater vehicles, understanding the evolution of form and function of swimming and flying organisms, understanding the neural control of movement (i.e. neuromechanics), among others. Our approach has also reached a wider scientific community, e.g., Greg Turk’s group in the Computer Science Department at Georgia Tech. has used it for physics–based animation of movie scenes. Our future focus is on the next grand challenge of developing a fully resolved neuromechanics simulator for self-propulsion where the neuronal models are fully coupled with our fully resolved simulation technique.